Quote from Matt Watts on September 25th, 2014, 12:32 PM

Here's a refresher video:

https://www.youtube.com/watch?v=DovunOxlY1k#ws

That is a great demonstration machine!  I'm going to be going off on a Rodin Math tangent on this one. :D But first I'm going to be very hypothetical.  Seems like our ossilly scopes need a screen on the back side of the box also. ;)

For EVERY action there is an equal but opposite reaction.  How long do we have to wait for the reaction?  Can it be happening at the same precise time as the action?  Does the reaction have to happen in a form observable to Humans by any means?

Notice he shows the camera side of the machine to demonstrate how the wave looks, but puts his terminating devices on the other wave on his side of the machine.  We are looking at the camera side of a wave on our ossilly scopes, completely ignoring the back side of the wave.  Sure its an equal but opposite wave, we can predict it, so it is easy to ignore it.   But I think in the video demonstration he proves the back side of the wave can be manipulated affecting the front of the wave with out notice, if  that is all  you are looking at.  Providing that we can apply this simple mechanical demonstration to all waves in nature as he says.


When I first seen him run a wave through the machine, I thought of this right away.  Many have wondered what this symbol looks like in 3D.  Some have tried to draw it as a sphere, I've thought about trying that myself.  The problem is the symbol doesn't represent a single static object.  It's showing a snapshot in time of perpetual movement.



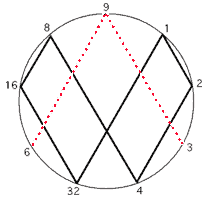
Well, I think we just seen it in 3D in the old ATT video.  I have some scribblings started to try and show that the symbol is really a sine wave with mirrored symmetry across a central axis (not a central plane).   I think this symbol is exactly the same as our modern day scope shot with the trigger set correctly.  All a scope is missing is the back side of the wave and the numbers in the right places on the wave. :) I'll be labelling my battery terminals 3 and 6 from now on. :P ;)


Nate

Great observation N8.  A transverse wave is always going to have an opposite side.  Now a longitudinal wave...   That's a different story.

The thing about the John Shive video is that these waves move slowly in comparison to waves propagating along a conductor.  Superposition is key, but what we see on the scope is the final result of millions of waves that have bounced from one end to the other at the speed of light.  And only one side of them at that.  We don't even see the J (imaginary) side as Dollard refers to it.  How on God's green earth can we ever slow this down enough to see the waves build up one at time, layer upon layer?

Looking forward to your Rodin Math 3D view.  :)

I think the wave at the rearside of his device is irrelevant in most cases, its just 180degrees out of phase with the front, he used some engenuity to make a wavemachine based on torque of the middle wire, the fact that it can be viewed from either side and see the same waveform I think in most cases is not important. There might be some specific cases where its useful but I cant think of any off top of my head.

Quote from Matt Watts on October 2nd, 2014, 10:31 PM

How on God's green earth can we ever slow this down enough to see the waves build up one at time, layer upon layer?

Looking forward to your Rodin Math 3D view.  :)

I don't think we every really will.  What is the possibility that there is more to view in a electrical wave if put in 3D? 

heres an interesting visualisation within a coaxial cable

https://www.youtube.com/watch?v=JFKZnwmb24o#

closest I could find to stans tube cells, theres quite a few videos of cfd simulations by the person who did the video above

   brettly,
interesting...

it is an interesting video, gives the possibility that inbetween the tubes of a hho cell is a very complex waveform. But..coax has positive in the centre, stans cell has negative in the centre.
The video above shows the wave starting as a point source half way between the inner and outer
tubes, also its only a 2d view, adding the length dimension would further complicate things.
So its not identical to stans cell, but does give the possibility that the waveform within the tube is
too complex to have practical relevance.
It may be there is no standing wave created  in stans tubes, it might not be importantespecially if there is a constantly changing series of complex nodes, as long as it works is all that matters.
Then again there is the possibility that the waveform is not as complex as in the video, since the waves are concentric originating from the outer positive wall (?) and travelling extremely quickly along the tube ( 1/9 speed of light), how the waves from the  two chokes interact within the cell
further complicates things. Seems stan gave the second choke less turns in his tube cells, but
went with identical chokes windings with the injectors, it might be the lower area of the injectors doesn't require adjusting second choke inductance, or maybe he found out later that
it doesn't matter if the second choke doesn't have lower inductance that first choke?

Quote from brettly on October 9th, 2014, 02:02 AM

Seems stan gave the second choke less turns in his tube cells, but
went with identical chokes windings with the injectors, it might be the lower area of the injectors doesn't require adjusting second choke inductance, or maybe he found out later that
it doesn't matter if the second choke doesn't have lower inductance that first choke?

good question, i have always wondered this. why different in all other systems but not i the injector...

more research to do on that one...

~Russ